Triangle circle construct circumscribed circumcenter constructions geometry mathbitsnotebook bisector draw perpendicular find math
Table of Contents
Table of Contents
In geometry, the circumcenter is the point of intersection where the perpendicular bisectors of a triangle meet. Drawing a circumcenter may seem intimidating at first, but it is a crucial skill that every geometry student must learn. In this article, we will guide you on how to draw a circumcenter and provide tips and tricks to help you master this concept.
One of the biggest challenges that geometry students face is understanding the concept of a circumcenter. It can be difficult to visualize where the perpendicular bisectors intersect, especially for complex triangles. Additionally, it can be confusing to know which tools to use for drawing a circumcenter.
Fortunately, drawing a circumcenter is not as complicated as it may seem. To draw a circumcenter, you will need a straightedge and a compass. You will also need to know how to construct perpendicular bisectors. By following a few simple steps, you can easily find the circumcenter of any triangle.
To find the circumcenter of a triangle, you will first need to construct the perpendicular bisectors of each side. This can be done using a compass to measure the same length from each endpoint of a side and then drawing the arc. Then, repeat this process with the other two sides. The circumcenter is the point where these perpendicular bisectors intersect.
My Personal Experience Drawing a Circumcenter
When I first learned about the circumcenter, I struggled to fully understand the concept. However, once I realized that it was simply the intersection of perpendicular bisectors, it became much easier to draw. I found that practicing on simple triangles helped me to build my skills for more complex ones. Drawing a circumcenter soon became second nature to me, and I was able to complete geometry problems with ease.
Tips and Tricks for Drawing a Circumcenter
One key tip to keep in mind when drawing a circumcenter is to be patient and take your time. Rushing through the construction process can lead to mistakes and frustration. Another helpful trick is to use graph paper to keep your lines straight and neat. Additionally, if you are struggling with a particularly complex triangle, try breaking it down into smaller triangles to make the process easier.
How to Use the Circumcenter in Geometry Problems
The circumcenter can be a useful tool in solving geometry problems. For example, it can be used to find the radius of a circumscribed circle, which is a circle that passes through all three vertices of a triangle. To find the radius, simply measure the distance between the circumcenter and one of the vertices. This distance is equal to the radius of the circumscribed circle.
Common Mistakes to Avoid When Drawing a Circumcenter
One common mistake that geometry students make when drawing a circumcenter is not constructing accurate perpendicular bisectors. Ensure that your arcs intersect at the same point, and that your bisectors are straight and meet at the same point. Another mistake is rushing through the construction process or not following the steps precisely. Take your time and double-check your work to avoid errors.
Troubleshooting Circumcenter Problems
If you are struggling to draw a circumcenter or have made a mistake in your construction, don’t panic. Go back to the beginning and ensure that your perpendicular bisectors are accurate. Check that your arcs intersect at the same point and that your bisectors are straight. If you still can’t find the circumcenter, try breaking the triangle down into smaller triangles to make the process easier.
Question and Answer
Q. How is the circumcenter different from the incenter in geometry?
A. While they may sound similar, the circumcenter and incenter are different points in a triangle. The incenter is the point where the angle bisectors of a triangle meet, while the circumcenter is the point where the perpendicular bisectors of a triangle meet.
Q. Can you find the circumcenter of a right triangle?
A. Yes, you can find the circumcenter of a right triangle. The circumcenter will be located at the midpoint of the hypotenuse.
Q. What is the circumcenter used for in geometry?
A. The circumcenter can be used to find the radius of a circumscribed circle and can also help in solving other geometry problems. Additionally, knowing how to draw a circumcenter is a fundamental skill that is necessary for understanding more complex geometric concepts.
Q. Do you need a compass to draw a circumcenter?
A. Yes, a compass is necessary for drawing a circumcenter as it is used to construct perpendicular bisectors. A straightedge is also helpful for drawing straight lines.
Conclusion of How to Draw Circumcenter
Drawing a circumcenter is an important skill that every geometry student must master. By following a few simple steps and taking your time to construct precise perpendicular bisectors, you can easily find the circumcenter of any triangle. Remember to be patient, use graph paper, and double-check your work to avoid errors. The circumcenter is a powerful tool in geometry, and being able to draw it accurately is essential for understanding more complex geometric concepts and solving geometry problems.
Gallery
Areas Of Quadrilaterals Within A Triangle Determined By Its

Photo Credit by: bing.com /
Pin By Julie Grant On Math & Teacher Fun :) | Geometry Lessons, Math

Photo Credit by: bing.com / circumcenter triangle construct compass mathopenref construction proof straightedge perpendicular constructing bisector geometry math argument ruler
Construct The Circumcenter Of A Triangle (examples, Solutions
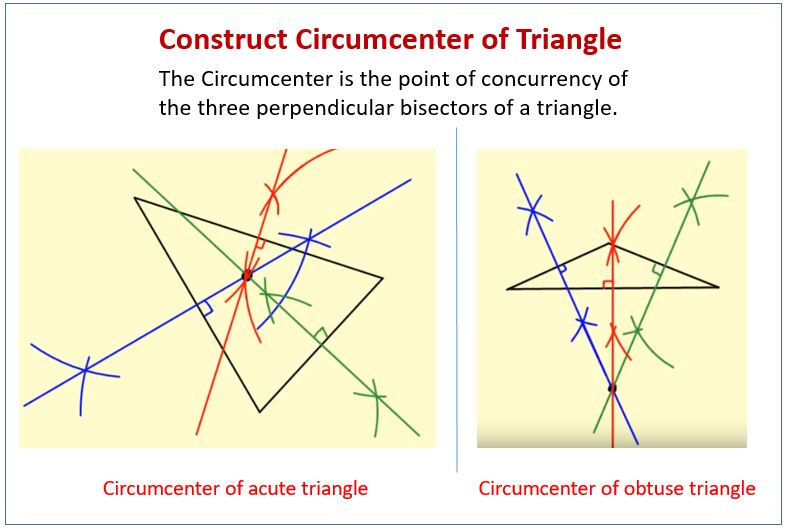
Photo Credit by: bing.com / circumcenter triangle construct find
Circumcenter Of A Triangle (examples, Solutions, Videos, Worksheets
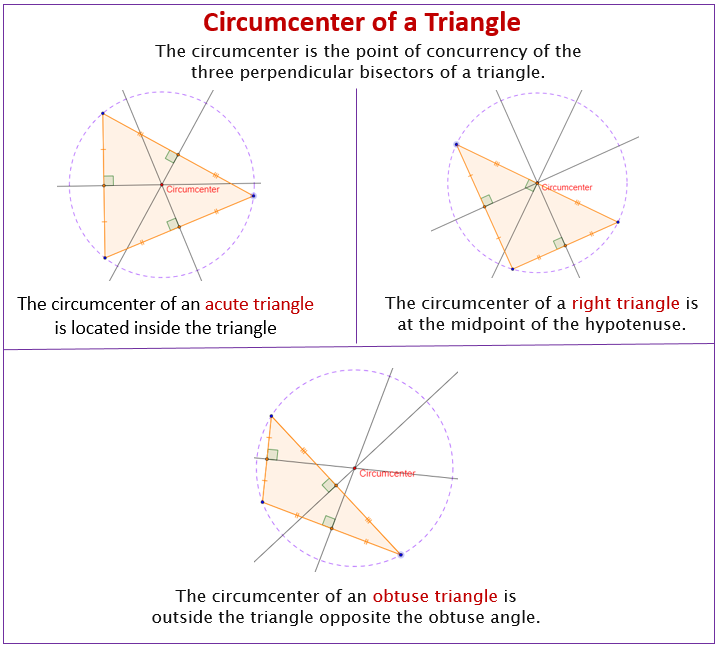
Photo Credit by: bing.com / circumcenter triangle obtuse triangles acute
Circumcenter - MathBitsNotebook (Geo - CCSS Math)
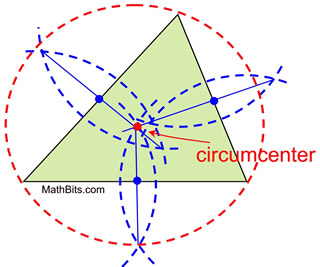
Photo Credit by: bing.com / triangle circle construct circumscribed circumcenter constructions geometry mathbitsnotebook bisector draw perpendicular find math